Answer for HW2

1

方法一：最小势能原理

方法二：虚功原理

以圆锥顶点为原点，竖直向下为 z 轴正方向，所以弹性圈的半径为 $r = z \tan α$ ，弹性圈上的质点坐标是：

{\vec{r}}_{i} = z {\hat{e}}_{z} + z \tan α {\hat{e}}_{r}

由 $δ {\hat{e}}_{r} = θ δ {\hat{e}}_{θ}$ ，于是虚位移满足：

δ {\vec{r}}_{i} = δ z \hat{e_{z}} + δ z \tan α \hat{e_{r}} + z \tan α δ θ \hat{e_{θ}}

拉伸后弹性圈的长度变为 $2 π z \tan α$ ，得到弹性圈上的一小段圆心角 $d θ$ 的圆弧受到的弹力是：

T_{i} = 2 T \sin \frac{d θ}{2} \approx T d θ = k (2 π z \tan α - l) d θ

得到其受到的主动力(重力+弹性力)是：

{\vec{F}}_{i} = \frac{d θ}{2 π} m g \hat{e_{z}} - d θ \cdot k (2 π z \tan α - l) \hat{e_{r}}

根据虚功原理：

0 = \sum_{i} {\vec{F}}_{i} \cdot δ {\vec{r}}_{i} = d θ δ z (\frac{m g}{2 π} - \tan α k (2 π z \tan α - l))

\Rightarrow z = \frac{m g + 2 π k l \tan α}{k (2 π \tan α)^{2}}

Info

两种方法都只适用于系统处于平衡的情况，在非平衡时，虚功原理进化为达朗贝尔原理，最小势能原理进化为拉格朗日方程。

2

以沿斜面向下为 x 正方向，圆柱转过的角度为 $θ$ ，转动惯量为 $I = \frac{1}{2} m R^{2}$ ，约束条件 $\dot{x} = R \dot{θ}$ ，柱心的虚位移是 $δ x$ ，圆柱上某个质点的位置分解为质心位置+到质心的位移 ${\vec{r}}_{i} = x {\hat{e}}_{x} + {\vec{r}}_{i}^{'}$ ：

{\vec{F}}_{i} = m_{i} \vec{g}

\dot{{\vec{r}}_{i}} = \dot{x} {\hat{e}}_{x} + r_{i}^{'} \dot{θ} {\hat{e}}_{θ} \Rightarrow \ddot{{\vec{r}}_{i}} = \ddot{x} {\hat{e}}_{x} + r_{i}^{'} \ddot{θ} {\hat{e}}_{θ} - r_{i}^{'} {\dot{θ}}^{2} {\hat{e}}_{r_{i}}^{'} = R \ddot{θ} e_{x} + r_{i}^{'} \ddot{θ} {\hat{e}}_{θ} - {\vec{r}}_{i}^{'} {\dot{θ}}^{2}

δ {\vec{r}}_{i} = δ x {\hat{e}}_{x} + r_{i}^{'} δ θ {\hat{e}}_{θ}

根据达朗贝尔原理（主动力和惯性力的虚功和为 0）：

\begin{aligned} 0 & = \sum_{i} ({\vec{F}}_{i} - m_{i} \ddot{{\vec{r}}_{i}}) \cdot δ {\vec{r}}_{i} \\ = M g \sin α δ x - \sum_{i} m_{i} (\ddot{x} {\hat{e}}_{x} + \ddot{{\vec{r}}_{i}^{'}}) \cdot δ (x {\hat{e}}_{x} + {\vec{r}}_{i}^{'}) \\ = M g \sin α δ x - M \ddot{x} δ x - 0 - 0 - \sum_{i} m_{i} \ddot{{\vec{r}}_{i}^{'}} \cdot δ {\vec{r}}_{i}^{'} \end{aligned}

其中最后一项：

\begin{aligned} \sum_{i} m_{i} \ddot{{\vec{r}}_{i}^{'}} \cdot δ {\vec{r}}_{i}^{'} & = \sum_{i} m_{i} (r_{i}^{'} \ddot{θ} {\hat{e}}_{θ} - {\vec{r}}_{i}^{'} {\dot{θ}}^{2}) \cdot r_{i}^{'} δ θ {\hat{e}}_{θ} \\ = \sum_{i} m_{i} {r_{i}^{'}}^{2} \ddot{θ} δ θ \\ = I \ddot{θ} δ θ \end{aligned}

得到：

M g \sin α δ x - M \ddot{x} δ x - I \ddot{θ} δ θ = 0

根据约束 $δ x = R δ θ ， \ddot{x} = R \ddot{θ}$ 得到：

δ x (M g \sin α - M \ddot{x} - \frac{I \ddot{x}}{R^{2}}) = 0 \Rightarrow \ddot{x} = \frac{M g \sin α}{M + \frac{1}{2} M} = \frac{2}{3} g \sin α

这是质心的运动方程，圆柱上质点只需要多加一个向心加速度。

3

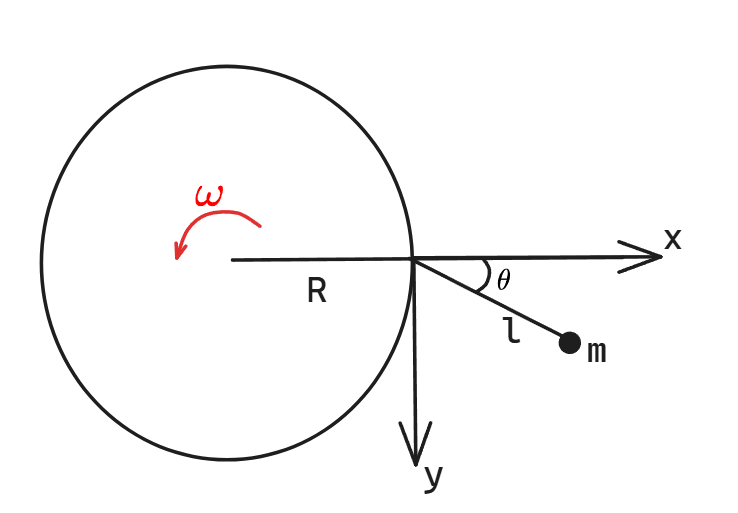
当系统处于稳定状态时，在圆盘的旋转参考系中，

\begin{aligned} x = l \cos θ, y = l \sin θ & \Rightarrow \dot{x} = - l \dot{θ} \sin θ, \dot{y} = l \dot{θ} \cos θ \\ \Rightarrow \ddot{x} = - l (\ddot{θ} \sin θ + {\dot{θ}}^{2} \cos θ), \ddot{y} = l (\ddot{θ} \cos θ - {\dot{θ}}^{2} \sin θ) \end{aligned}

δ x = - l \sin θ δ θ, δ y = l \cos θ δ θ

\vec{F} = m ω^{2} (\vec{R} + \vec{l}) ， 惯 性 离 心 力

于是：

\begin{aligned} 0 & = (\vec{F} - m \ddot{\vec{r}}) \cdot δ \vec{r} \\ = (F_{x} - m \ddot{x}) δ x + (F_{y} - m \ddot{y}) δ y \\ = - m [ω^{2} R + l \cos θ + l (\ddot{θ} \sin θ + {\dot{θ}}^{2} \cos θ)] l \sin θ δ θ + m [l \sin θ - l (\ddot{θ} \cos θ - {\dot{θ}}^{2} \sin θ)] l \cos θ δ θ \end{aligned}

化简得到：

0 = l \ddot{θ} + ω^{2} R \sin θ

等价于在 $\vec{g} = - ω^{2} \vec{R}$ 引力场中的运动。